Что такое вращающийся блок? Как рассчитать объем тела вращения?
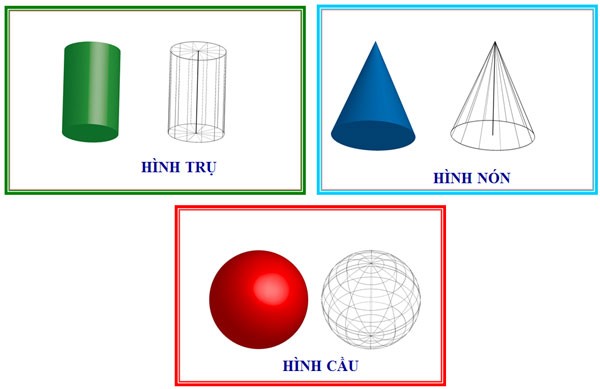
Тело вращения — это фигура, созданная вращением плоскости вокруг фиксированной оси, например, конус вращения, цилиндр вращения, сфера вращения и т. д. Ниже приведена формула для расчета объема тела вращения, пожалуйста, ознакомьтесь с ней.
Оглавление
Если круглый блок вращается вокруг оси Ox, то для расчета объема вращающегося круглого блока можно применить следующие формулы:
Случай 1 : Вращающийся круговой блок, созданный:
Тогда формула для расчета объема будет следующей:
Случай 2 : Вращающийся блок создается путем:
Тогда формула для расчета объема тела вращения будет иметь вид:
с
Если круглый блок вращается вокруг оси Oy, то для расчета объема вращающегося круглого блока можно применить следующие формулы:
Случай 1 : Вращающийся блок создается путем:
Тогда формула для расчета объема тела вращения будет иметь вид:
Случай 2 : Вращающийся блок создается
Тогда объем тела вращения составит:
с
Сводная таблица формул для расчета объема тела вращения:
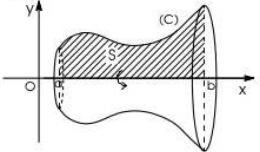
1. Vx, генерируемая областью S, вращающейся вокруг Ox:
Рецепт :
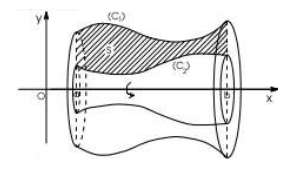
2. Vx, генерируемая областью S, вращающейся вокруг Ox:
Рецепт :
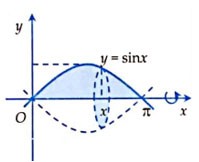
Пример 1:
Вычислить объем тела вращения, полученного вращением плоской фигуры, ограниченной кривой y = sinx, осью x и двумя прямыми x=0, x=π (чертеж), вокруг оси Ox.
Решение
Применяя формулу из приведенной выше теоремы, имеем
Пример 2:
Вычислите объем тела вращения, полученного вращением плоской фигуры, ограниченной кривой и осью x, вокруг оси x.
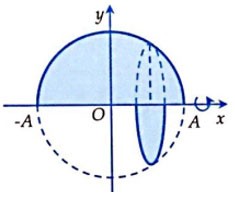
Приз:
Мы видим:
Таким образом, для всех x это уравнение полуокружности с центром O и радиусом R = A, лежащей выше оси Ox. При вращении вокруг оси Ox плоская фигура образует сферу с центром O и радиусом R = A (рисунок). Поэтому у нас всегда есть
Таким образом, в этом типе задач нам не нужно записывать формулу интегрирования, а можно сделать вывод на основе формулы для вычисления объема сферы.
Пример 3:
Рассчитайте объем тела, лежащего между двумя плоскостями x = 0 и x = 1, зная, что поперечное сечение тела, высеченное плоскостью (P), перпендикулярной оси Ox, в точке с абсциссой x(0≤x≤1), представляет собой прямоугольник с длинами двух сторон x и ln(x2+1).
Приз:
Поскольку поперечное сечение прямоугольное, площадь поперечного сечения равна:
У нас есть объем для расчета как
Пример 4: Дана плоская фигура, ограниченная линиями y = 3x; у = х; х = 0; x = 1 вращается вокруг оси Ox. Рассчитайте объем полученного тела вращения.
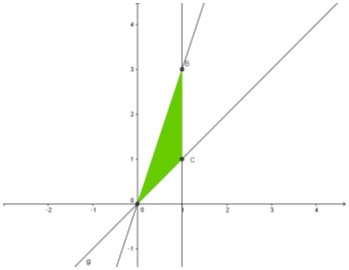
Приз:
Координатами пересечения прямой x = 1 с y = x и y = 3x являются точки C(1;1) и B(3;1). Координаты пересечения прямой y = 3x с y = x равны O(0;0).
Таким образом, объем вращающегося твердого тела, который необходимо рассчитать, равен:
Пример 5 : Дана плоская фигура, ограниченная линиями y = 2x2; y2 = 4x вращается вокруг оси Ox. Рассчитайте объем полученного тела вращения.
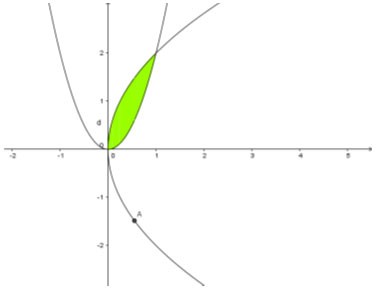
Приз:
С эквивалентным временем. Координаты пересечения прямой с — точки O(0;0) и A(1;2).
Таким образом, объем вращающегося твердого тела, который необходимо рассчитать, равен:
Для задач, требующих вычисления объема тела вращения, вам просто нужно использовать правильную формулу для каждого случая и быть внимательным при определении предела, чтобы иметь возможность решить ее. Удачи!
Возникли проблемы с ошибкой в руководстве по использованию Microsoft Teams? Узнайте о проверенных пошаговых способах её быстрого устранения. Очистка кэша, обновление и многое другое для беспроблемного начала работы. Работает на последних версиях!
Устали от ошибок воспроизведения мультимедиа в Microsoft Teams, которые портят ваши встречи в 2026 году? Следуйте нашему пошаговому руководству от экспертов, чтобы быстро устранить неполадки со звуком, видео и обменом файлами — никаких технических навыков не требуется. Вас ждет бесперебойное сотрудничество!
Возникли проблемы с ошибкой прокси-сервера Microsoft Teams? Ознакомьтесь с проверенными шагами по устранению неполадок с настройками прокси-сервера Microsoft Teams. Очистите кэш, настройте параметры прокси-сервера и вернитесь к бесперебойным звонкам за считанные минуты с помощью нашего руководства от экспертов.
Устали от ошибок синхронизации задач в Microsoft Teams, которые мешают вашей работе? Следуйте нашим пошаговым инструкциям, чтобы восстановить бесперебойную синхронизацию задач между Teams, Planner и To Do. Быстрые решения для мгновенного облегчения!
Найдите точное расположение ключей реестра Microsoft Teams в Windows 11. Пошаговое руководство по поиску, доступу и безопасному изменению этих ключей для оптимальной производительности и устранения неполадок. Незаменимо для ИТ-специалистов и энтузиастов Teams.
Проблемы с медленной работой Microsoft Teams? Узнайте, как пошагово очистить кэш Microsoft Teams, чтобы устранить проблемы с производительностью, задержки, сбои и повысить скорость работы на Windows, Mac, в веб-версии и на мобильных устройствах. Быстрые и эффективные решения!
Возникла проблема с загрузкой вкладки Wiki в Microsoft Teams? Узнайте о проверенных пошаговых решениях, которые помогут быстро устранить проблему, восстановить вкладки Wiki и без лишних хлопот повысить производительность команды.
Раздражает отсутствие значка Microsoft Teams в Outlook? Узнайте, где именно его найти, почему он исчезает, и проверенные шаги по его восстановлению для беспроблемных встреч. Обновлено для последних версий!
Разочарованы отсутствием комнат для обсуждений в вашей встрече Teams? Узнайте о главных причинах, по которым вы не видите комнаты для обсуждений в Teams, и следуйте нашим пошаговым инструкциям, чтобы они заработали за считанные минуты. Идеально подходит как для организаторов, так и для участников!
Устали от ошибки Microsoft Teams 1200, которая прерывает ваши телефонные звонки? Узнайте о быстрых пошаговых решениях для iOS и Android, чтобы быстро восстановить бесперебойную командную работу — никаких технических навыков не требуется!
Откройте для себя простые пошаговые инструкции по отключению Microsoft Teams при запуске системы и повышению производительности ПК. Более быстрая загрузка, меньшее потребление ресурсов — идеально для пользователей Windows, стремящихся к плавной работе.
Узнайте самый простой способ загрузить Microsoft Teams для Mac, MacBook Air и MacBook Pro. Пошаговые инструкции, системные требования и советы по устранению неполадок для беспроблемной установки последней версии. Начните прямо сейчас!
Не можете найти папку установки Microsoft Teams на своем компьютере? Это пошаговое руководство покажет точные пути для новых и классических версий Teams, а также для установки на одного пользователя и на весь компьютер. Сэкономьте время на устранении неполадок!
Научитесь легко присоединяться к собраниям Microsoft Teams с помощью идентификатора и пароля на компьютере, мобильном устройстве или в веб-версии. Пошаговые инструкции со скриншотами для быстрого доступа — приглашение не требуется!
Узнайте, как эффективно использовать фоновые изображения Microsoft Teams с помощью пошаговых инструкций, советов по загрузке и лучших практик, чтобы сделать ваши видеозвонки профессиональными и увлекательными. Поднимите свой уровень удаленной работы на новый уровень уже сегодня!
