Формула для вычисления высоты в правильных, равнобедренных, равносторонних и прямоугольных треугольниках

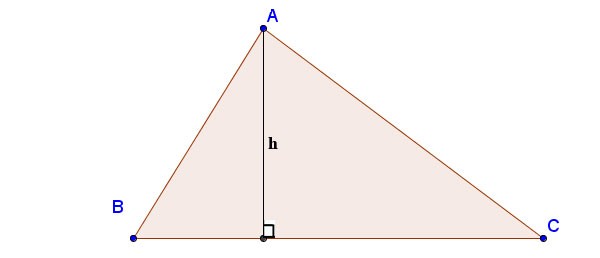
Высота в треугольнике — это прямая линия с важными свойствами, тесно связанная с задачами плоской геометрии. Так чему же равна высота, как вычислить высоту в треугольнике? Ответ и простейшую формулу для расчета высоты треугольника можно найти в статье ниже.

Оглавление

• Формула расчета высоты в треугольнике
  • Вычислите высоту в правильном треугольнике
  • Вычислите высоту в равностороннем треугольнике
  • Формула для расчета высоты в прямоугольном треугольнике
  • Формула для вычисления высоты в равнобедренном треугольнике
• Определение высоты в треугольнике
• Свойства трех высот треугольника

Формула расчета высоты в треугольнике

Вычислите высоту в правильном треугольнике

Как вычислить высоту треугольника по формуле Герона:

Где a, b, c — длины сторон; ha — высота, проведенная из вершины A к стороне BC; p — полупериметр:

Например: 

Дан треугольник ABC, сторона AB = 4 см, сторона BC = 7 см, сторона AC = 5 см. Вычислите высоту AH из точки A, пересекающую BC в точке H, и вычислите площадь ABC.

Приз:

Половина периметра треугольника: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(см)

Высота   

=>

Рассмотрим треугольник ABC, имеем:

Так,

Вычислите высоту в равностороннем треугольнике

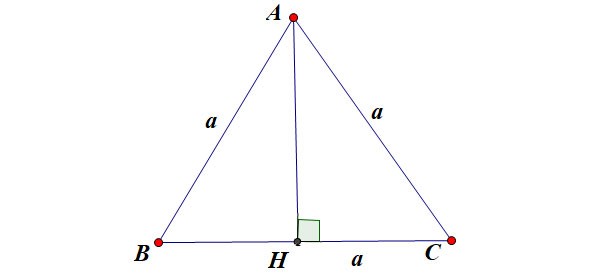
Предположим, что равносторонний треугольник ABC имеет длину стороны a, как показано на рисунке:

Там:

• h — высота равностороннего треугольника
• а — длина стороны равностороннего треугольника

Формула для расчета высоты в прямоугольном треугольнике

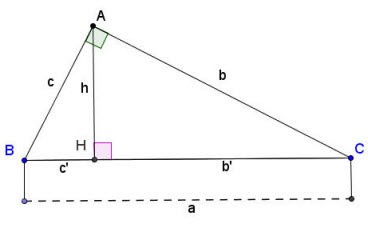
Предположим, что в точке A расположен прямоугольный треугольник ABC, как показано выше:

Формула для расчета сторон и высот в прямоугольном треугольнике:

1. а2 = б2 + с2

2. b2 = ab′ и c2 = ac′

3. ах = бк

4. h2 = b′.c'

5.

Там:

• a, b, c — стороны прямоугольного треугольника, как показано выше;
• b' — проекция ребра b на гипотенузу;
• c' — проекция ребра c на гипотенузу;
• h — высота прямоугольного треугольника, проведенная из вершины прямого угла A вниз к гипотенузе BC.

Пример 1: Дан треугольник ABC с прямым углом A и высотой AH. Рассчитайте BC, AC, AH, зная, что AB = 15 см, HC = 16 см.

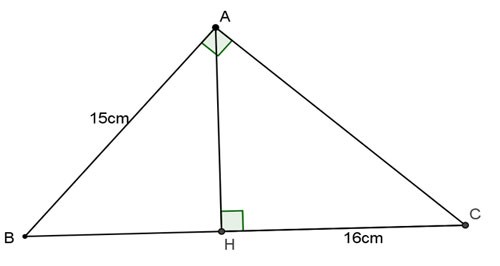
Приз:

Применяя алгебраическую формулу в прямоугольном треугольнике ABC, имеем:

AC2 = CH.BC = 16.BC

Согласно теореме Пифагора для прямоугольного треугольника ABC с прямым углом A имеем:

АВ2 + АС2 = ВС2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ БК(БК - 25) + 9(БК - 25) = 0

⇔ (БК - 25)(БК + 9) = 0

⇔ BC = 25 или BC = -9 (исключить)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (см)

Рассмотрим прямоугольный треугольник ABC с: AH.BC = AB.AC (геометрическая формула)

=> AH = AB.AC/BC = 15,20/25 = 12 (см)

Итак, BC=25(см); АС=20(см); AH=12(см)

Пример 2 :

Дан треугольник ABC — прямоугольный, сторона A равна 24 см, сторона AC равна 32 см. Перпендикуляр к BC пересекает AC, BC в точках D и E соответственно. Рассчитайте DE.

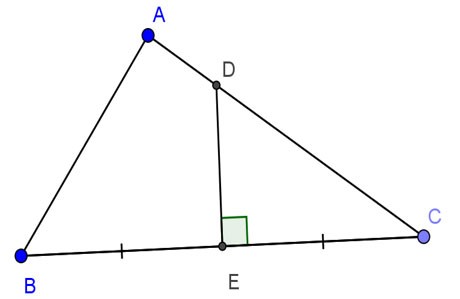
Приз:

Рассмотрим прямоугольный треугольник ABC. Имеем:

BC2 = AB2 + AC2 (по теореме Пифагора)

ВС2 = 242+ 322

БК2 = 1600

ВС = 40(см)

EC = BC : 2 = 40 : 2 = 20(см)

Рассмотрим прямоугольный треугольник ACB и прямоугольный треугольник ECD с:

Есть ∠A = ∠E = 90o

∠C общий

=> Треугольник ACB ∾ треугольник ECD (gg)

=> АС/ЕС = АВ/ЕД

=> ED = AB.EC/AC = 15 см

Итак, ED = 15 см.

Формула для вычисления высоты в равнобедренном треугольнике

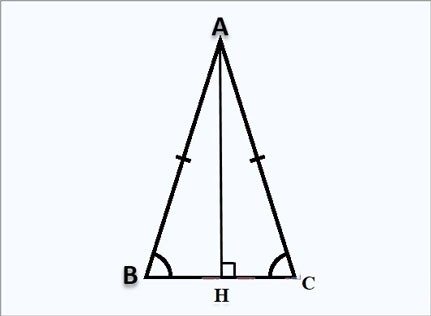
Предположим, у вас есть равнобедренный треугольник ABC в точке A, высота AH перпендикулярна точке H, как показано выше:

Формула для расчета высоты AH:

Поскольку треугольник ABC является равнобедренным в точке A, высота AH также является медианой, поэтому:

⇒ НВ=НС= ½ВС

Применяя теорему Пифагора в прямоугольном треугольнике ABH в точке H, имеем:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Например : Δ ABC уравновешен в точке A с BC = 30 (см), высота AH = 20 (см). Вычислите высоту, соответствующую стороне этого равнобедренного треугольника.

Решение: Рассмотрим Δ ABC — равнобедренный треугольник в точке A с BC = 30(см)

⇒ BH = CH = 15(см).

Применяя теорему Пифагора, имеем:

Теперь нам нужно вычислить BK = ?

У нас есть:

С другой стороны

Поэтому имеем ⇔

Определение высоты в треугольнике

Высота в треугольнике — это перпендикулярный отрезок, проведенный из вершины к противоположной стороне. Эта противоположная сторона называется основанием, соответствующим высоте. Длина высоты — это расстояние между вершиной и основанием.

Свойства трех высот треугольника

Три высоты треугольника проходят через одну и ту же точку. Эта точка называется ортоцентром треугольника .

Вам просто нужно вычислить неизвестные компоненты в приведенных выше формулах для вычисления высоты треугольника, чтобы иметь возможность вычислить высоту треугольника.

• На чем делается акцент? Формула для расчета центра тяжести т��еугольника