Что такое рациональное число? Что такое иррациональное число?

Определения и формулы рациональных и иррациональных чисел являются важными знаниями в математике, которые учащиеся должны понимать, чтобы иметь прочную математическую базу. В следующей статье вы познакомитесь с определением, свойствами и математическими формами рациональных и иррациональных чисел. Пожалуйста, ознакомьтесь с ним.

Рациональные числа, иррациональные числа

• Что такое рациональное число?
  • Классификация рациональных чисел
  • Представление рациональных чисел на числовой прямой
  • Сложение и вычитание рациональных чисел
  • Умножение и деление рациональных чисел
  • Абсолютное значение рационального числа
  • Сравните два рациональных числа
  • Формула для вычисления степени рационального числа
• Что такое иррациональное число?
  • Понятие иррациональных чисел
  • Свойства иррациональных чисел
• В чем разница между рациональными и иррациональными числами?
• Взаимосвязь множеств чисел
• Упражнения на рациональные числа

Что такое рациональное число?

- Рациональные числа — это множество чисел, которые можно записать в виде дробей (частных). То есть рациональное число можно представить бесконечной периодической десятичной дробью.

- Рациональные числа записываются как , где a и b — целые числа, но b должно быть отлично от 0.

- это множество рациональных чисел.

=> Множество рациональных чисел: .

Например: , , … — рациональные числа.

• Любое целое число a является рациональным числом, поскольку целое число a можно записать в виде .

Например: У нас есть рациональные числа.

У нас есть:

Комментарий: все числа рациональные.

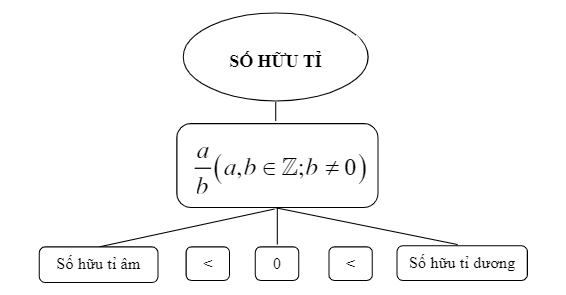
Классификация рациональных чисел

Рациональные числа делятся на два типа: отрицательные рациональные числа и положительные рациональные числа. Конкретно:

• Отрицательные рациональные числа: включают рациональные числа меньше 0.
• Положительные рациональные числа: включают рациональные числа больше 0.

Примечание: Число 0 не является ни отрицательным рациональным числом, ни положительным рациональным числом.

Природа

• Множество рациональных чисел является счетным множеством.
• Коммутативное свойство:
• Свойство сложения с 0:
• Комбинированные свойства:

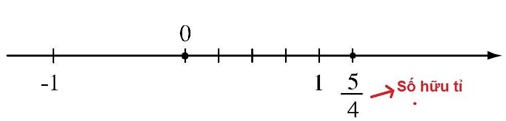
Представление рациональных чисел на числовой прямой

- Для представления рациональных чисел на числовой прямой мы следуем следующим факторам:

Шаг 1: Запишите рациональное число в виде дроби.

Шаг 2: Разделите единичный отрезок на b равных частей, чтобы получить новый единичный отрезок, который является старой единицей.

Шаг 3: Рациональное число представлено точкой А, находящейся на расстоянии a новых единиц от точки 0.

• Если число А отрицательное, оно находится слева от 0.
• A находится справа от 0, если это положительное число.

Например: На рисунке точка P представляет рациональное число:

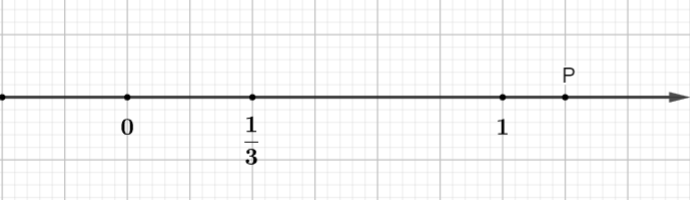
Инструктировать

Отрезок единичной линии делится на 6 равных частей (новая единица составляет 1/6 старой единицы)

Точка P расположена на расстоянии 7 новых единиц от точки O.

А точка P находится справа от точки O, поэтому P — положительное рациональное число.

Итак, P представляет собой рациональное число.

Сложение и вычитание рациональных чисел

i) Правила сложения и вычитания двух рациональных чисел

Мы можем складывать и вычитать два рациональных числа x и y, записывая их в виде двух дробей, а затем применяя правила сложения и вычитания дробей.

У нас есть:

ii) Свойства

- Сложение рациональных чисел обладает свойствами сложения дробей: коммутативность, ассоциативность, сложение с 0, сложение с обратными числами.

- У нас есть:

а) Коммутативное свойство:

б) Ассоциативные свойства:

в) Добавить 0:

г) Добавьте противоположное число:

iii, Правила перехода

При перемещении члена из одной части уравнения в другую мы должны изменить знак этого члена.

В Q у нас есть алгебраическая сумма, в которой мы можем менять члены местами, расставлять скобки, чтобы группировать члены произвольно, подобно алгебраическим суммам в наборе целых чисел.

• С если тогда
• У нас есть:

Умножение и деление рациональных чисел

i) Правила умножения и деления двух рациональных чисел

- Мы можем умножить и разделить два рациональных числа, записав их в виде дробей, а затем применив правила умножения и деления дробей.

• У нас есть:
• У нас есть:

Например:

Умножение рациональных чисел: 

Деление рациональных чисел: 

ii) Свойства

- Умножение рациональных чисел имеет те же свойства, что и умножение дробей: коммутативность, ассоциативность, умножение на 1 и распределительное свойство умножения относительно сложения.

- Каждое ненулевое рациональное число имеет обратное.

- У нас есть:

• Коммутативное свойство: .
• Ассоциативные свойства: .
• Свойство умножения на 1: .
• Распределительные свойства: .
• С . Обратной величиной для a является .

Абсолютное значение рационального числа

- Абсолютное значение рационального числа a, обозначаемое как , представляет собой расстояние от точки a до точки 0 на числовой прямой.

Например:

(Потому что )

(Потому что )

Сравните два рациональных числа

- С любыми двумя рациональными числами мы всегда имеем или или .

- Чтобы сравнить два рациональных числа, делаем следующее:

• Запишите в виде двух дробей с одинаковым положительным знаменателем:
• Сравните числители как целые числа a, b:

Например: Сравните два рациональных числа: и

У нас есть:

Потому что это хорошо.

Формула для вычисления степени рационального числа

Формулы для вычисления степеней рациональных чисел, которые вам нужно запомнить

• Произведение двух степеней с одинаковым основанием:
• Сила власти
• Мощность продукта
• Степень частного

Что такое иррациональное число?

Понятие иррациональных чисел

• Упоминая рациональные числа, нельзя не упомянуть иррациональные числа. Это числа, записанные в виде бесконечных неповторяющихся десятичных дробей, обозначаемых .
• Действительные числа, не являющиеся рациональными, не могут быть представлены в виде отношений.

Например: 3,145248… — иррациональное число.

Свойства иррациональных чисел

Множество иррациональных чисел является несчетным множеством.

Например:

Иррациональные числа: 0,1010010001000010000010000001… (это бесконечная непериодическая десятичная дробь)

Количество квадратных корней: √2 (квадратный корень)

Пи (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

В чем разница между рациональными и иррациональными числами?

• Рациональные числа включают в себя бесконечные повторяющиеся десятичные дроби, в то время как иррациональные числа — это бесконечные неповторяющиеся десятичные дроби.
• Рациональные числа — это просто дроби, в то время как иррациональные числа имеют много различных типов чисел.
• Рациональные числа — это счетные числа, а иррациональные числа — это несчетные числа.

Взаимосвязь множеств чисел

Символы наборов чисел:

• N: Множество натуральных чисел
• N*: Множество натуральных чисел, отличных от 0
• Z: Набор целых чисел
• В: Множество рациональных чисел
• I: Множество иррациональных чисел

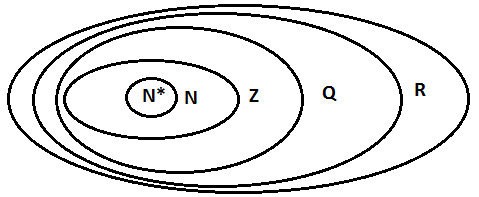
Имеем: R = Q ∪ I.

Установите N; Z ; В; Р.

Тогда отношение включения между множествами чисел имеет вид: N ⊂ Z ⊂ Q ⊂ R

Упражнения на рациональные числа

Форма 1: Выполнение вычислений с рациональными числами

Метод решения: Для решения упражнений по выполнению вычислений, связанных с рациональными числами, сначала преобразуйте рациональные числа в дроби, затем примените правила вычислений при сложении, вычитании, умножении и делении рациональных чисел.

Пример: Рассчитать  

Отвечать:

Форма 2: Представление рациональных чисел на числовой прямой

Решение: Вам необходимо определить, является ли рациональное число положительным рациональным числом или отрицательным рациональным числом, а затем продолжить, выполнив следующие шаги:

• Если рациональное число a/b является положительным рациональным числом: На числовой прямой, в положительном направлении, разделите длину 1 единицы на b равных частей. Затем возьмем точку на положительном направлении оси Ox, укажем часть и определим положение рационального числа a/b.
• Если рациональное число a/b является отрицательным рациональным числом: На числовой прямой, в отрицательном направлении оси, разделите длину 1 на b равных частей. Затем возьмем точку на отрицательном направлении оси Ox, укажем часть и определим положение рационального числа a/b.

Форма 3: Сравнение рациональных чисел

Решение: Преобразуйте данные рациональные числа в дроби с одинаковым положительным знаменателем, затем сравните числители. Более продвинутые пользователи могут сравнить их с дробями среднего уровня, чтобы найти ответ.

Форма 4: Определите, является ли рациональное число отрицательным, положительным или 0.

Метод решения: Для решения упражнений 4-го типа учащимся необходимо на основе свойств рациональных чисел определить, является ли рациональное число отрицательным, положительным или 0.

Например: дано рациональное число x = (a – 25)/29. Определите значение a так, чтобы:

• x отрицательный
• x положительный
• х = 0

Отвечать:

x — отрицательное число => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x — положительное число => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

х = 0 => (а – 25)/29 =0 0 => а – 25 = 0 => а = 25

Форма 5: Найти рациональные числа в интервале согласно заданным условиям

Решение: Если в задаче требуется найти рациональные числа в интервале в соответствии с заданными условиями, то для нахождения ответа нам нужно подставить рациональные числа в один и тот же числитель или знаменатель.

Пример: Найдите значение m для значений «больше» и «меньше»

Руководство по ответам

Преобразуйте дроби к общим знаменателям следующим образом:

Общий знаменатель: 18

Согласно вопросу имеем:

Форма 6: Найдите x с помощью рациональных чисел

Метод решения математических задач: Для решения математических задач по нахождению x с рациональными числами необходимо выполнить приведение к общему знаменателю и преобразовать x в одну сторону, а оставшиеся члены в 1. Отсюда вычислить значение x.

Например: Найдите x, зная x. (2/ 3) + 5/ 6 = 1/ 8

Отвечать:

х . (2/ 3) + 5/ 6 = 1/ 8

=> х. (2/ 3) = 1/ 8 + 5/ 6

=> х = 46/ 48 : 2/ 3

=> х = 23 . 3 / 24 . 2

=> 23/16

Форма 7: Найдите a так, чтобы выражение было целым числом

Метод решения математических задач: Для задачи нахождения числа а, если числитель не содержит а, нужно воспользоваться знаком делимости. Если числитель содержит букву a, используйте знак делимости или разделите числитель знаменателем. Если задача требует одновременного нахождения a и b, сгруппируйте a или b и преобразуйте их в дробную форму для вычисления.

Пример: Найдите целое число a при условии, что 8/(a – 1) является целым числом.

Отвечать:

Условие: а – 1 ≠ 0 => а ≠ 1

Пусть a будет целым числом => 8 делится на (a – 1)

=> (a – 1) является множителем 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (а – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> а = {-7, -3, -1, 0, 3, 5, 9}

Надеюсь, статья выше помогла вам понять, что такое рациональные числа, что такое иррациональные числа, типы рациональных чисел, что такое символы рациональных чисел и как распознавать рациональные числа, чтобы легко решать задачи.

В дополнение к знаниям об иррациональных числах и рациональных числах, приведенным выше, вы можете обратиться к некоторым другим математическим знаниям, таким как обыкновенные дроби , смешанные числа , десятичные дроби ...