Формула расчета диагонали ромба

Ромб — это четырёхугольник с четырьмя равными сторонами, четырёхугольник с двумя диагоналями, перпендикулярными друг другу в средней точке каждой линии, — это ромб, параллелограмм с двумя равными смежными сторонами... Помимо квадратов, прямоугольников, треугольников... ромб является одной из важных фигур в математике и жизни.

Помимо формулы вычисления периметра и площади ромба , большое значение имеет также способ вычисления диагонали ромба — линии, соединяющей противоположные вершины ромба.

Статья ниже поможет вам научиться вычислять диагональ ромба на конкретных примерах, пожалуйста, обратитесь к ней.

Оглавление

• Диагональ ромба
• Свойства диагоналей ромба
• Формула расчета диагонали ромба
• Задача на вычисление диагонали ромба

Диагональ ромба

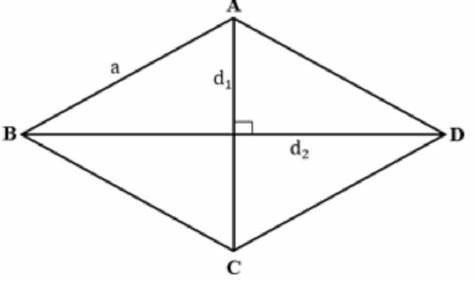
• Диагональ ромба — это линия, соединяющая две противоположные вершины ромба.
• Ромб имеет две диагонали, пересекающиеся в середине ромба.
• Диагональ делит ромб на два равносторонних треугольника с равными сторонами.

Свойства диагоналей ромба

Две диагонали в ромбе обладают следующими свойствами:

• Две равные диагонали: Две диагонали ромба имеют одинаковую длину.
• Угол между двумя диагоналями является прямым углом: Две диагонали ромба пересекаются в его середине и образуют прямой угол.
• Диагонали являются осями симметрии ромба: Каждая диагональ ромба является осью симметрии ромба, делящей ромб на две симметричные половины.
• Диагонали являются диагоналями двух равносторонних треугольников: Каждая диагональ ромба является диагональю двух равносторонних треугольников, образованных равными сторонами.
• Произведение длин двух диагоналей равно произведению длин двух сторон ромба: Произведение длин двух диагоналей равно произведению длин двух сторон ромба. То есть, если обозначить диагональ через d, а стороны через a и b, то получим d² = a² + b².

Эти свойства являются характерными свойствами ромбов и используются во многих геометрических задачах, связанных с ромбами.

Формула расчета диагонали ромба

Пожалуйста, рассмотрите приведенный ниже пример, чтобы вывести формулу для расчета диагонали ромба.

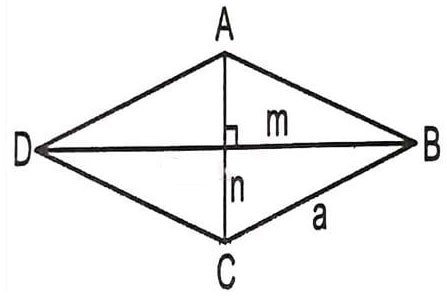
Предположим, нам нужно вычислить длину диагонали ромба ABCD со стороной a и углом ABC = 60 градусов -> какова формула вычисления диагонали ромба в этом случае?

Решение:

Так как ABCD — ромб, все стороны равны a.

Рассмотрим треугольник ABC, где: AB = BC = a.

Еще раз: ABC = 60 градусов => Треугольник ABC — равносторонний треугольник со стороной a.

=> АВ = АС = ВС = а

=> Длина диагонали ромба равна AC = BD = a.

Приведенное выше решение является одной из самых простых и понятных формул для вычисления диагонали ромба.

Формула для вычисления диагонали ромба, если известна площадь и оставшаяся диагональ

Из формулы расчета площади ромба:

S = (axb) : 2

У нас есть следующая формула для длины диагонали:

а = S x 2 : b

или

б = С х 2 : а

Там:

• S — площадь
• a и b — длины двух диагоналей

Используйте геометрические свойства ромба, чтобы вычислить длину диагонали, не прибегая к теореме Пифагора. Конкретно:

Диагональ ромба равна среднему значению двух его высот.

Диагональ = квадратный корень из (длинная высота + короткая высота)²

Диагональ ромба равна половине периметра ромба.

Диагональ = 1/2 x периметр ромба.

Задача на вычисление диагонали ромба

Задача 1: Дан ромб площадью 360 квадратных сантиметров и длиной диагонали 24 сантиметра. Рассчитайте длину второй диагонали.

Решение:

По формуле площади ромба: axb : 2

У нас есть вторая диагональ: 360 x 2 : 24 = 30 см.

Ответ: 30см

Проблема 2:

Площадь ромба равна 4 дм, длина одной диагонали равна 3/5 дм. Вычислите длину второй диагонали. Решение:

Длина второй диагонали равна:

(4 x 2) : 3/5 =40/3 (дм)

Урок 3: Две диагонали ромба имеют длину 160 см и 120 см. Вычислите высоту ромба, зная, что соотношение высоты и длины стороны ромба равно 24:25.

Решение:

Площадь ромба равна: 160,120:2 = 9 600 (см2).

Поскольку соотношение высоты и длины стороны ромба равно 24:25, то можно считать, что высота ромба равна 24а, а сторона ромба равна 25а.

Тогда имеем площадь ромба: 25а.24а = 9 600 а2 = 16 а = 4 см2.

Высота ромба равна: 24,4 = 96 (см).

Итак, высота ромба равна 96 см.

Урок 4: 

Дан ромб ABCD со стороной 12,5 см, высотой 6,72 см, причем AC меньше BD. Каковы длины диагоналей AC и BD соответственно?

Приз:

Применим формулу для расчета площади ромба: S = ha = 6,72 x 12,5 = 84 см2.
=> 1/2 АС x BD = 84 => 2АС.BD = 336

Пусть О — пересечение двух диагоналей ромба.

У нас AOB — прямоугольный треугольник с точкой O, поэтому AB2 = OA2 + OB2

Где OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (Согласно задаче BD > AC) (2)

Из (1) и (2) имеем:

BD = 24, AC = 7см.

Урок 5: 

Ромб ABCD имеет стороны, равные 10 единицам. Вычислите длину диагонали ромба.

Решение: Длина диагонали ромба ABCD равна:

Диагональ = квадратный корень из 2(10²) = квадратный корень из 200 = 14,14 единиц длины.

Таким образом, длина диагонали ромба ABCD составляет 14,14 единиц длины.

Урок 6:

Ромб ABCD имеет диагональ 12 единиц. Вычислите периметр ромба.

Решение: Поскольку ромб имеет четыре равные стороны, его периметр будет равен сумме длин четырех сторон, то есть:

Периметр = 4 x длина стороны = 4 x 6 = 24 единицы длины.

Таким образом, периметр ромба ABCD равен 24 единицам длины.