Формула для расчета площади поверхности и объема сферы

Давайте изучим и рассмотрим формулу для расчета площади поверхности и объема сферы с помощью Quantrimang.com в статье ниже.

Оглавление

• Что такое сфера?
  • Что такое сфера?
• Формула для расчета площади поверхности и объема сферы
  • Формула для расчета площади поверхности сферы
  • Формула для расчета объема шара:
• Формула для расчета радиуса сферы
  • Сфера, описывающая пирамиду, имеет сторону, перпендикулярную основанию.
  • Квадратный тетраэдр (это частный случай формулы 1)
  • Вертикальная призма имеет основание, представляющее собой вписанный многоугольник.
  • Формула тетраэдра, вершины которого являются вершинами прямой призмы
  • Формула для расчета радиуса сферы для пирамиды с боковыми гранями, перпендикулярными основанию
• Примеры расчета площади поверхности и объема сферы

Что такое сфера?

Сфера — это геометрическое место точек, равноудалённых от заданной фиксированной точки O rв трёхмерном пространстве. Точка О называется центром, а расстояние rназывается радиусом сферы.

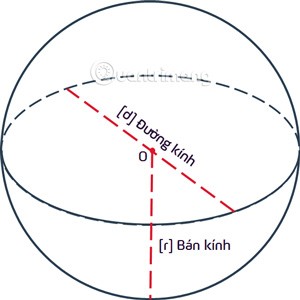
Что такое сфера?

Сфера — это множество точек, лежащих внутри сферы, а сферой называется сфера или сфера с центром O и радиусом r = OA.

Формула для расчета площади поверхности и объема сферы

Формула для расчета площади поверхности сферы

Площадь поверхности сферы в четыре раза больше площади большого круга, которая в четыре раза больше постоянной Пи, умноженной на квадрат радиуса сферы.

Формула для расчета объема шара:

Объем сферы, также известный как объем сферы, рассчитывается путем умножения трех четвертей числа Пи на куб радиуса сферы.

Там:

• Sэто площадь поверхности сферы
• Vобъем сферы
• rэто радиус сферы/сферы
• dэто сфера/сфера

Формула для расчета радиуса сферы

Сфера, описывающая пирамиду, имеет сторону, перпендикулярную основанию.

• Rd — радиус основания.
• h — длина стороны, перпендикулярной основанию.

Например : Дана пирамида S.ABCD с прямоугольным основанием, где AB = 3a, BC = 4a, SA = 12a и SA перпендикулярна основанию. Вычислите радиус R сферы, описанной около пирамиды S.ABCD.

Решение: У нас есть

Так

Квадратный тетраэдр (это частный случай формулы 1)

Квадратный блок OABC имеет OA, OB, OC, перпендикулярные друг другу, и имеет:

Например:

Тетраэдр OABC имеет взаимно перпендикулярные OA, OB, OC и радиус описанной сферы . Наибольший объем тетраэдра OABC

Решение : У нас есть

С другой стороны, у нас есть:

Согласно неравенству AM - GM имеем:

Вертикальная призма имеет основание, представляющее собой вписанный многоугольник.

Там:

• Rd — радиус основания
• h — длина стороны.

Пример 1: Дана сфера радиуса R, описывающая куб со стороной a. Какое из следующих утверждений верно?

А.

Б.

С.

Д.

Решение: У нас есть

Итак, ответ — С.

Формула тетраэдра, вершины которого являются вершинами прямой призмы

Тетраэдр (H1) имеет вершины, которые являются вершинами вертикальной призмы (H2), тогда:

Формула для расчета радиуса сферы для пирамиды с боковыми гранями, перпендикулярными основанию

Где R, d — радиус основания; a, x — соответственно длина пересечения боковой грани и основания, угол при вершине боковой грани, смотрящий вниз на основание.

Или вы можете использовать формулу

Где: Rb — радиус описанной окружности боковой грани, а a — длина пересечения боковой грани и основания.

Например: 

Дана пирамида S.ABCD с квадратным основанием, равносторонний треугольник SAD со стороной √2a, лежащий в плоскости, перпендикулярной основанию. Вычислите радиус R сферы, описанной около пирамиды S.ABCD.

А.

Б.

Решение: У нас есть

Поэтому правильный ответ — Б.

Примеры расчета площади поверхности и объема сферы

Урок 1 : Дан круг длиной 31,4 см. Вычислите объем сферы, радиус которой равен радиусу данной окружности.

Приз:

Длина окружности C = 2πr = 31,4 см

=> Радиус r = C/2π = 5 см

Объем данной сферы равен:

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523,3 см³

Урок 2 : Вычислите объем шара диаметром d = 4 см.

Приз:

Радиус r = d/2 = 2 см

Объем сферы равен:

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33,49 см³

Урок 3 :

Пусть окружность диаметром 4а вращается вокруг своего диаметра. Каков тогда объем вращающегося твердого тела?

Решение: Если взять окружность диаметром 4a, вращающуюся вокруг своего диаметра, то получится сфера диаметром 4a или радиусом R = 2a.

Объем сферы равен:

Урок 4 :

Сфера радиусом R√3 имеет площадь:

А. 4√3πR2

Б. 4πR2

С. 6πR2

D. 12πR2

Решение: Применяем формулу: S = 4πR2

Площадь поверхности сферы радиусом R√3 равна: S = 4π(R√3)2 = 12πR2

Итак, ответ — D.

Две короткие формулы, но запомнить их надолго довольно сложно. Добавьте статью в закладки и откройте ее, когда она вам понадобится. Надеюсь, эта статья будет вам полезна.

В дополнение к формуле для расчета площади поверхности и объема сферы, приведенной выше, вы также можете обратиться к формуле для расчета площади некоторых других основных фигур, таких как треугольники , прямоугольники и параллелограммы. ..