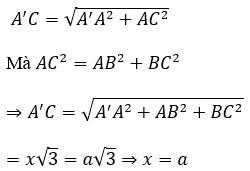Призма — многоугольник с двумя параллельными и равными основаниями и боковыми гранями в форме параллелограмма.
Комментарий:
- Боковые грани призмы равны и параллельны друг другу.
- Боковые грани — параллелограммы.
- Два основания призмы представляют собой два равных многоугольника.
Какова формула для расчета объема призмы (V-образной призмы) и какова формула для расчета объема вертикальной призмы? Пожалуйста, обратитесь к статье ниже.
Оглавление
1. Объем вертикальной призмы
Формула для расчета объема вертикальной призмы:
Объем прямой призмы равен произведению площади основания на высоту.
Там
Vобъем призмы (единица м3)Bэто площадь основания (единица м2)hвысота призмы (единица измерения м)
3. Классификация призм
Правильная призма
Представляет собой вертикальную призму с основанием в виде правильного многоугольника. Боковые грани призмы — все равные прямоугольники. Например: правильная треугольная призма, правильный четырехугольник... тогда мы понимаем это как правильную призму.
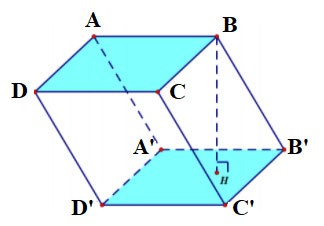
Правильная четырехугольная призма называется правильной четырехугольной призмой.
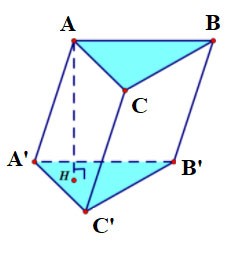
Треугольная призма
- Треугольная призма имеет 5 граней, 9 ребер и 6 вершин.
- Оба основания треугольные и параллельны друг другу; Каждая боковая грань представляет собой прямоугольник;
- Стороны равны;
- Высота треугольной призмы равна длине одной стороны.
Например:
Треугольная призма ABC.A'B'C' имеет:
- Нижнее основание - треугольник ABC, верхнее основание - треугольник A'B'C';
Боковые грани — прямоугольники: AA'B'B, BB'C'C, CC'A'A;
- Края:
- Базовые ребра: AB, BC, CA, A'B', B'C', C'A'
- Стороны: AA', BB', CC';
- Вершины: A, B, C, A', B', C'.
- Высота — это длина одной стороны: AA' или BB' или CC'.
Четырехугольная призма
- Четырехугольная призма имеет 6 граней, 12 ребер и 8 вершин.
- Оба основания являются четырехугольниками и параллельны друг другу. Каждая боковая грань представляет собой прямоугольник.
- Стороны равны.
- Высота четырехугольной призмы равна длине одной стороны.
Например:
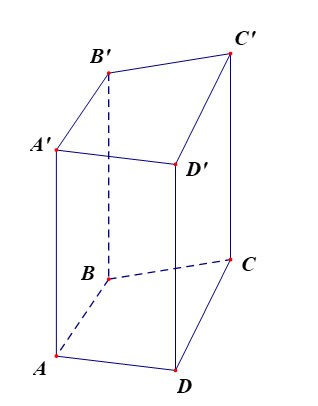
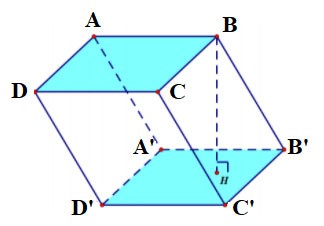
Четырехугольная призма ABCD.A'B'C'D' имеет:
- Нижнее основание - четырехугольник ABCD, верхнее основание - четырехугольник A'B'C'D';
Боковые грани — прямоугольники: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Края:
+ Базовые ребра: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Боковые грани: AA', BB', CC', DD' равны.
- Вершины: A, B, C, D, A', B', C', D'.
- Высота — это длина одной стороны: AA' или BB' или CC' или DD'.
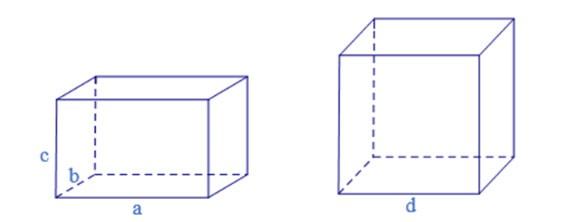
Примечание: Прямоугольные призмы и кубы также являются четырехугольными призмами.
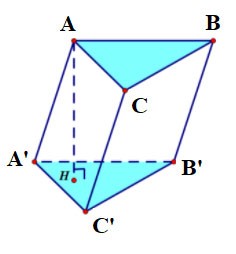
Правая призма
Если боковые грани призмы перпендикулярны основанию, она называется прямой призмой.
Примечание:
Если основание представляет собой прямоугольник, то вертикальный цилиндр четырехугольника называется прямоугольным параллелепипедом.
Если четырехугольный цилиндр имеет 12 сторон длиной a, то его название — куб.
Сравните правильную призму и обычную призму:
| ОПРЕДЕЛЯТЬ: |
ПРИРОДА |
| + Вертикальная призма — это призма, сторона которой перпендикулярна основанию. |
+ Боковые грани вертикальной призмы прямоугольные.
+ Боковые грани призмы перпендикулярны основанию.
+ Высота - это сторона
|
| + Правильная призма — вертикальная призма, основанием которой является правильный многоугольник. |
+ Боковые грани призмы — все равные прямоугольники.
+ Высота - это сторона
|
4. Пример расчета объема вертикальной призмы
Пример 1:
Дана призма ABC.A'B'C', основание ABC которой представляет собой равносторонний треугольник со стороной a = 2 см и высотой h = 3 см. Рассчитайте объем этой призмы?
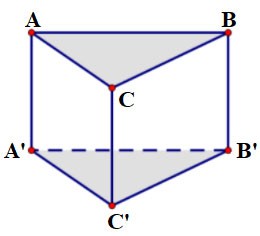
Приз:
Поскольку основание представляет собой равносторонний треугольник со стороной a, площадь равна:
В это время объем призмы равен:
Пример 2:
Упражнение 1: Дан вертикальный параллелепипед с ребрами AB = 3a, AD = 2a, AA'= 2a. Рассчитайте объем блока A'.ACD'
Инструктировать:
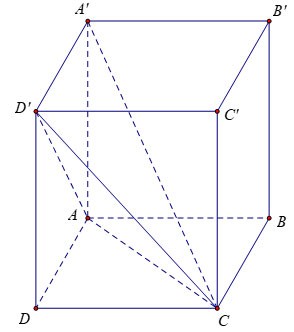
Поскольку боковая грань ADD'A' представляет собой прямоугольник, то имеем:
Пример 3 : Дана вертикальная призма ABC.A'B'C', основание которой представляет собой равносторонний треугольник со стороной a√3, угол между основанием и призмой равен 60º. Пусть M будет серединой BB'. Рассчитайте объем пирамиды M.A'B'C'.
Приз:
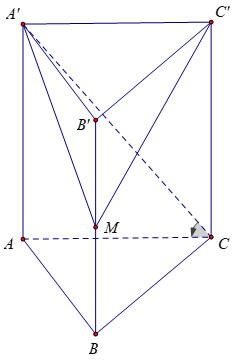
Следовательно, мы можем сделать вывод, что
У нас есть:
Пример 4:
Дана правильная четырехугольная призма ABCD.A'B'C'D' с основанием длиной a и гранью (DBC'), составляющей угол 60º с основанием ABCD. Рассчитайте объем призмы ABCD.A'B'C'D?
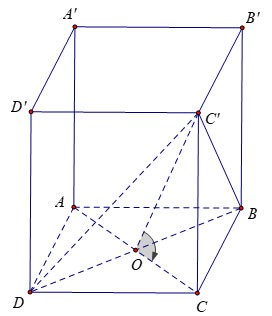
Имеем: в центре O квадрата ABCD.
С другой стороны, поэтому
Вывод
Также:
Пример 5:
Рассчитайте объем V куба ABCD.A'B'C'D', зная AC'=a√3
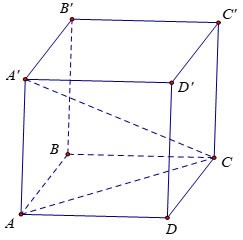
Приз:
Пусть x — длина стороны куба.
Рассмотрим треугольник AA'C с прямым углом A, где:
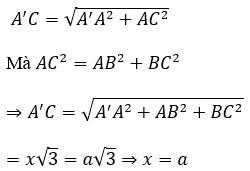
Следовательно, объем куба равен V=a^3.
В дополнение к формуле для расчета объема призмы, приведенной выше, вы можете обратиться к другим статьям о формуле для расчета объема тела вращения , формуле для расчета площади и длины окружности круга ...