Формула вычисления площади и периметра параллелограмма является базовым знанием. Пожалуйста, воспользуйтесь формулой, составленной Quantrimang.com ниже.
Оглавление
1. Площадь параллелограмма
Площадь параллелограмма измеряется размером площади поверхности, которая представляет собой видимую плоскую часть параллелограмма.
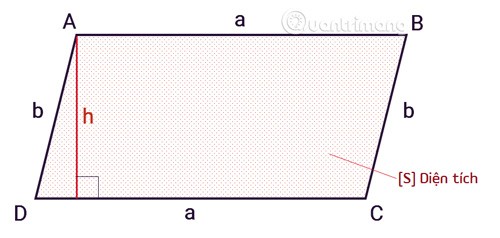
Площадь параллелограмма вычисляется по формуле, равной произведению основания на высоту.
SABCD = ахх
Там:
Sплощадь параллелограмма.aявляется основанием параллелограмма.hвысота параллелограмма от вершины до основания.
2. Периметр параллелограмма
Периметр параллелограмма вычисляется путем сложения длин линий, окружающих фигуру, которая также является линией, окружающей всю площадь, равной 2, умноженным на сумму любой пары смежных сторон.
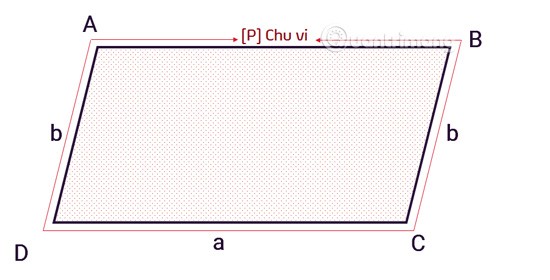
Другими словами, периметр параллелограмма равен сумме длин четырех сторон. Конкретная формула выглядит следующим образом:
С = 2 х (а+b)
Там:
Cпериметр параллелограмма.aи bявляются смежными сторонами параллелограмма.
3. Что такое параллелограмм?
Определять
Параллелограмм — четырёхугольник с 2 парами параллельных сторон или с 1 парой параллельных и равных сторон. Параллелограмм имеет два равных противолежащих угла и две диагонали, пересекающиеся в середине фигуры.
Параллелограмм можно считать частным случаем трапеции.
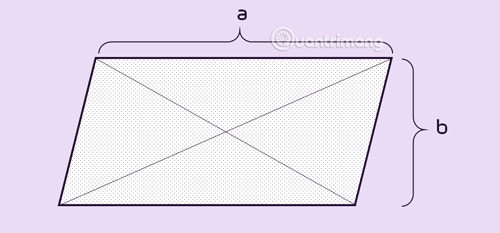
Свойства параллелограмма
В параллелограмме:
- Противоположные стороны равны.
- Противоположные углы равны.
- Две диагонали пересекаются в середине каждой линии.
ABCD — параллелограмм, AC пересекает BD в точке O. Тогда:
• АВ = СD, АД = ВС
•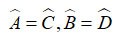
• ОА = ОС, ОБ = ОД
Знаки признания
а) Четырехугольник, у которого противоположные стороны параллельны, является параллелограммом.
б) Четырехугольник, у которого противоположные стороны равны, является параллелограммом.
в) Четырехугольник, у которого две противоположные стороны параллельны и равны, является параллелограммом.
г) Четырехугольник, у которого противолежащие углы равны, является параллелограммом.
д) Четырехугольник, две диагонали которого пересекаются в середине, является параллелограммом.
4. Вопросы с несколькими вариантами ответов для проверки параллелограммов
Упражнение 1 : Выберите неправильное предложение.
A. Параллелограмм имеет две диагонали, пересекающиеся в середине каждой диагонали.
B. Параллелограмм имеет два равных противолежащих угла.
C. Параллелограмм имеет две диагонали, перпендикулярные друг другу.
D. Два параллелограмма имеют две пары параллельных противоположных сторон.
Решение
В параллелограмме:
+ Параллелограмм имеет противоположные стороны параллельные
+ Противоположные стороны равны
+ Две диагонали пересекаются в середине каждой линии, поэтому утверждение C неверно.
Правильный ответ: С
Упражнение 2 : Дан параллелограмм ABCD, где Â = α > 900. Вне параллелограмма начертите равносторонние треугольники ADE, ABF. К какому типу треугольников относится треугольник CEF? Выберите лучший ответ
А. Треугольник
B. Равнобедренный треугольник
C. Равносторонний треугольник
D. Тупоугольный треугольник
Отвечать:
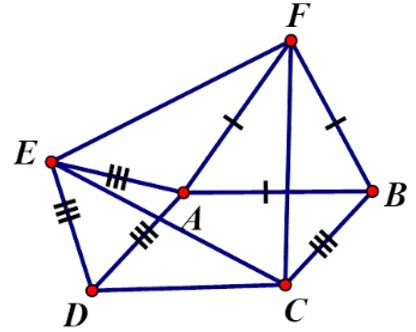

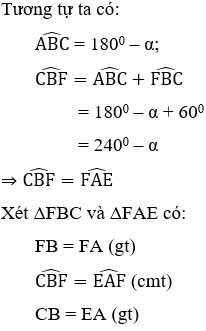
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
Из (1) и (2) можно вывести, что CF = FE = EC, поэтому треугольник CEF равносторонний.
Урок 3 : Выберите неправильное предложение. ABCD — параллелограмм. Затем:
А. АВ = СD
Б. н.э. = до н.э.
C. Тест на параллелограмм с ответами
D. АС = BD
Решение
В параллелограмме:
+ Параллелограмм имеет противоположные стороны параллельные
+ Противоположные стороны равны
+ Две диагонали пересекаются в середине каждой линии, поэтому D неверен.
Урок 4 : Заполните пропуск соответствующей фразой: «Четырехугольник с двумя диагоналями… является параллелограммом».
А. равный
B. пересекаются
C. пересекаются в середине каждой линии
D. параллельно
Решение
Признаки:
Четырехугольник, две диагонали которого пересекаются в середине каждой, является параллелограммом.
Урок 5 : Выберите неправильное предложение:
А. Четырехугольник с двумя парами параллельных противолежащих сторон является параллелограммом.
Б. Трапеция с двумя равными углами, прилежащими к основанию, является параллелограммом.
C. Четырехугольник с двумя парами равных противолежащих сторон является параллелограммом.
D. Четырехугольник с двумя парами равных противолежащих углов является параллелограммом.
Решение
Признаки:
+ Четырехугольник с противоположными параллельными сторонами является параллелограммом, поэтому утверждение A верно.
+ Четырехугольник с равными противоположными сторонами является параллелограммом, поэтому D верно.
+ Четырехугольник, у которого противоположные углы равны друг другу, является параллелограммом, поэтому D верно.
Понимая, что трапеция с двумя равными углами, прилежащими к основанию, является равнобедренной трапецией, поэтому утверждение B неверно.
Правильный ответ: Б.
5. Примеры вычисления периметра и площади параллелограмма
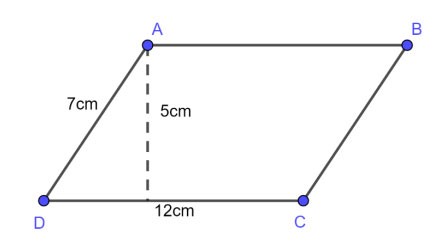
Пример 1 : Дан параллелограмм с основанием 12 см, стороной 7 см и высотой 5 см. Вычислите периметр и площадь этого параллелограмма?
Приз:
Периметр параллелограмма равен:
Р = 2 х (12 + 7) = 38 (см)
Площадь параллелограмма равна:
S = axh = 12 x 5 = 60 (см2)
Пример 2:
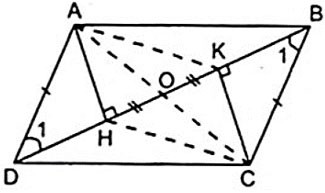
Дан параллелограмм ABCD, где H и K являются основаниями высот, проведенных из вершин A, C к BD соответственно.
а) Докажите, что AHCK — параллелограмм.
б) Пусть O — середина HK. Докажите, что A, O, C лежат на одной прямой.
Инструктировать:
а) Из гипотезы имеем:
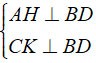 ⇒ АХ//СК. ( 1 )
⇒ АХ//СК. ( 1 )
Применяя свойства сторон параллелограмма и свойства накрест лежащих углов, имеем:
 ⇒ Δ АДГ = Δ ЦБК
⇒ Δ АДГ = Δ ЦБК
(случай гипотенузы – острого угла)
⇒ AH = CK (соответствующие стороны равны) ( 2 )
Из (1) и (2) следует, что четырехугольник AHCK с равными и параллельными противоположными сторонами является параллелограммом.
б) Применить свойства диагоналей параллелограмма AHCK
Параллелограмм AHCK имеет две диагонали AC и HK, пересекающиеся в середине каждой линии. Поскольку O является серединой HK, O также является серединой AC.
⇒ A, O, C находятся на одной прямой.
Помимо параллелограммов, формулы для вычисления площади и периметра других распространенных геометрических фигур, таких как ромбы , квадраты , трапеции , прямоугольники ... также очень важны и широко применяются в учебе и жизни.
Надеюсь, благодаря приведенной выше статье вы лучше поняли и усвоили основные знания о параллелограммах. Если у вас есть вопросы или комментарии для обсуждения с Quantrimang.com, оставьте комментарий ниже.



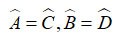



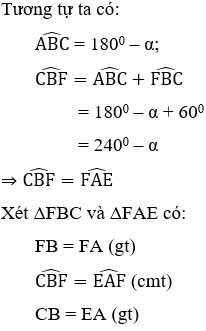


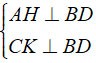 ⇒ АХ//СК. ( 1 )
⇒ АХ//СК. ( 1 ) ⇒ Δ АДГ = Δ ЦБК
⇒ Δ АДГ = Δ ЦБК