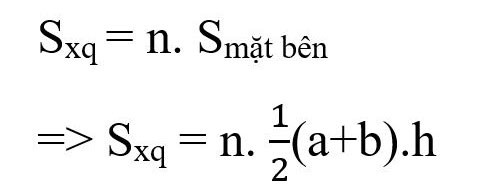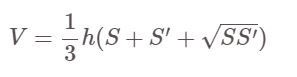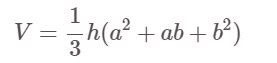Давайте узнаем в статье ниже, что такое усеченная пирамида, как вычислить объем усеченной пирамиды, площадь боковой поверхности и полную площадь усеченной пирамиды.
Оглавление
Определение термина усеченный конус
Усеченная пирамида — часть многогранника, расположенная между основанием и сечением, проведенным плоскостью, параллельной основанию пирамиды.
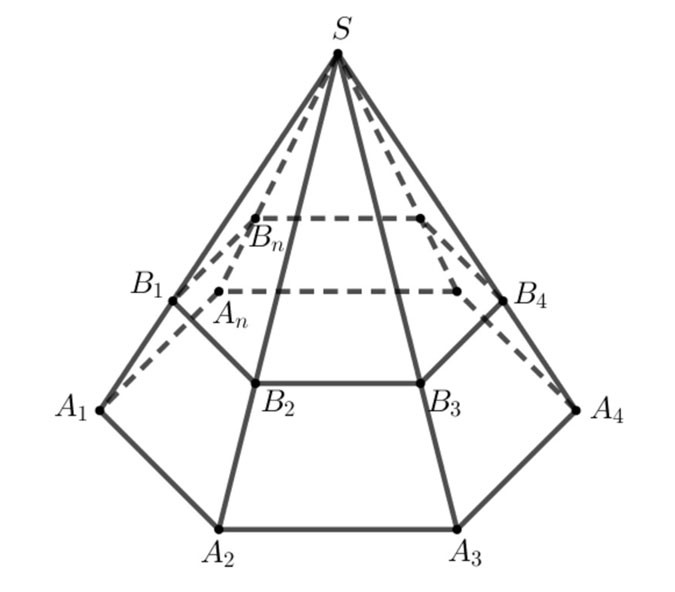
- Фигура, состоящая из многоугольников A1A2...An,B1B2...BnA1A2...An,B1B2...Bn и трапеций A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn называется усеченной пирамидой и обозначается как A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
- Проще говоря, усеченная пирамида образуется из пирамиды S.A1A2...AnS.A1A2...An после усечения пирамиды S.B1B2...Bn.S.B1B2...Bn.
+ Многоугольники A1A2...An,B1B2...BnA1A2...An,B1B2...Bn называются двумя основаниями,
+ Трапеции A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn называются боковыми гранями.
+ Отрезки прямых A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn называются боковыми ребрами, края базовой поверхности называются базовыми ребрами.
+ Расстояние между двумя основаниями называется высотой усеченной пирамиды.
Свойства усеченной пирамиды:
- Два основания представляют собой два многоугольника (треугольника, четырехугольника, пятиугольника и т. д.) с соответствующими параллельными сторонами и равными соотношениями соответствующих сторон.
- Боковые грани представляют собой трапеции.
- Линии, содержащие боковые ребра, сойдутся в одной точке (вершине пирамиды).
- Усеченная пирамида — это пирамида, основания которой представляют собой правильные многоугольники (с равными сторонами). Следовательно, все боковые грани усеченного треугольника представляют собой равные трапеции.
Формула для расчета площади усеченной пирамиды
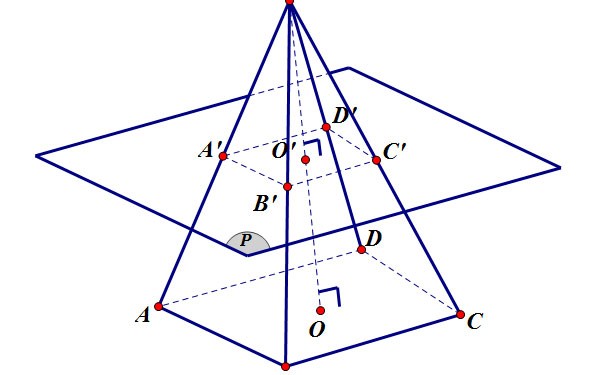
Площадь поверхности усеченной пирамиды
Площадь боковой поверхности усеченной пирамиды равна площади граней, окружающих усеченную пирамиду, за исключением площади двух оснований.
Как вычислить боковую площадь усеченной пирамиды: Вычислите площадь каждой боковой грани (трапеции) усеченной пирамиды по формуле вычисления площади нормальной трапеции , затем вычислите общую площадь.
Формула для расчета площади правильной усеченной пирамиды:
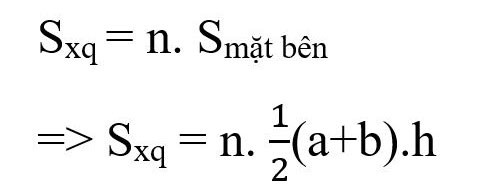
Там:
- Sxq: окрестности
- n: число боковых граней усеченной пирамиды (равное числу ребер базового многоугольника)
- a, b: длины сторон верхнего и нижнего оснований соответственно
- h: высота боковых четырехугольников.
Пример 1:
Вычислите боковую площадь правильной четырехугольной усеченной пирамиды с основаниями длиной 10 см и 15 см и высотой стороны 12 см.

Приз:
Боковая грань правильной четырехугольной усеченной пирамиды представляет собой равнобедренную трапецию, поэтому площадь одной боковой грани равна:
Правильная четырехугольная усеченная пирамида имеет 4 равные стороны, поэтому ее боковая площадь равна:
150 x 4 = 600 (см2)
Пример 2: Вычислите боковую площадь правильной четырехугольной усеченной пирамиды с ребрами основания 6 см и 8 см и высотой стороны 5 см. Вычислите боковую площадь правильной четырехугольной усеченной пирамиды с основаниями длиной 6 см и 8 см.

Приз:
Боковая грань правильной четырехугольной усеченной пирамиды — равнобедренная трапеция, поэтому площадь одной боковой грани равна
Правильная четырехугольная усеченная пирамида имеет четыре равные стороны, поэтому ее боковая площадь равна
35 х 4 = 140 (см2)
Полная площадь поверхности усеченной пирамиды
Общая площадь усеченной пирамиды равна сумме площади боковой поверхности и площади двух оснований.
Формула: Stp = Sxq + Большое дно + Малое дно
Там:
- Stp: Общая площадь
- Sxq: Окрестности
- Большая база: Большая площадь основания
- Маленькая база: Маленькая площадь базы
Например:
Рассчитайте полную площадь правильной усеченной пирамиды по размерам, указанным на рисунке.
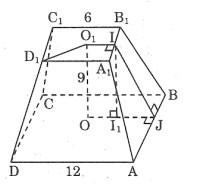
Приз:
У нас есть:
АД = 12 ⇒ ОЖ = 6
Нарисуем II1 ⊥ OJ, получим: I1J = 3
Применяя теорему Пифагора к прямоугольному треугольнику II1J, имеем:
IJ2 = II12 + I1J2 = 92 + 32 = 90
Следовательно:
Площадь одной стороны трапеции равна:
Окружающая площадь равна:
Площадь верхнего основания равна: S = 6 x 6 = 36 (единиц)
Площадь нижнего основания равна: S = 12 x 12 = 144 (единиц)
Полная площадь усеченной пирамиды равна:
Формула для расчета объема усеченной пирамиды
Рецепт:
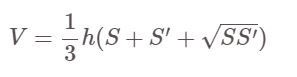
Там:
- V: объем усеченной пирамиды
- S, S' — площади большого и малого оснований пирамиды соответственно.
- h: высота пирамиды, то есть расстояние между двумя большими и малыми основаниями
Является ли усеченная пирамида квадратом (правильным четырехугольником):
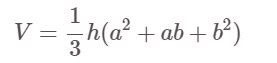
Там:
- V: Громкость
- h: Высота пирамиды
- a, b — длины рёбер большого основания и малого основания соответственно.