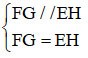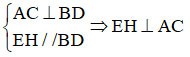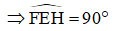Как вычислить диагональ квадрата, как вычислить диагональ прямоугольника часто используется в математических задачах и практических приложениях, таких как проектирование и строительство, срезание углов, измерение... Quantrimang.com собрал знания о свойствах двух диагоналей, а также формулы расчета, которые можно использовать в учебе, жизни и работе.
Оглавление
Какова диагональ квадрата и прямоугольника?
Диагональ квадрата или прямоугольника — это линия, соединяющая два противоположных угла. Каждый квадрат и прямоугольник имеет две диагонали одинаковой длины.
Как вычислить диагональ квадрата
Свойства диагонали квадрата
- Две диагонали квадрата равны по длине, перпендикулярны и пересекаются в средней точке каждой.
- Имеется вписанная окружность и описанная окружность, центры обеих окружностей совпадают и являются пересечением двух диагоналей квадрата.
- 1 диагональ разделит квадрат на два прямоугольных равнобедренных треугольника.
- Пересечение биссектрис, медиан и серединных перпендикуляров совпадает в одной точке.
- Обладает всеми свойствами прямоугольника, параллелограмма и ромба.
Формула расчета диагонали квадрата
Согласно свойствам квадрата, две диагонали квадрата равны, а одна диагональ квадрата делит квадрат на две части равной площади, которые представляют собой два равнобедренных прямоугольных треугольника. Таким образом, диагональ квадрата является гипотенузой двух равнобедренных прямоугольных треугольников.
Таким образом, чтобы вычислить диагональ квадрата, вам просто нужно применить теорему Пифагора к прямоугольному треугольнику.
Предположим, у вас есть квадрат ABCD со стороной длиной a, диагональ AC делит квадрат на два прямоугольных треугольника ABC и ACD.
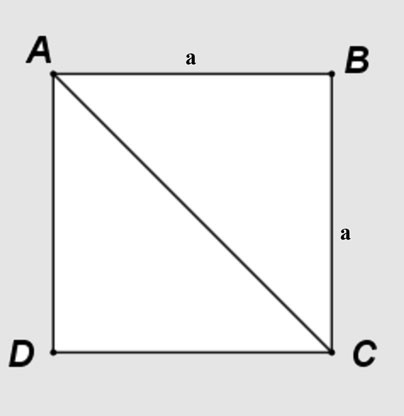
Применяем теорему Пифагора к прямоугольному равнобедренному треугольнику ABC:
⇒ ⇒
Итак, диагональ квадрата имеет длину стороны a:
Пример вычисления диагонали квадрата
Пример 1: сторона квадрата равна 3 см. Диагональ этого квадрата равна: 6 см, √18 см, 5 см или 4 см?
Решение:
а) Применяя теорему Пифагора к квадрату ABC, имеем:
AC² = AB² + BC² = 3² + 3² = 18
=> АС = см
Итак, диагональ квадрата равна √18 см.
Пример 2:
Диагональ квадрата равна 2дм. Сторона этого квадрата равна: 1 см, 3/2 см, √2 см или 4/3 см?
Приз:
Применим теорему Пифагора к прямоугольному треугольнику ABC, но в этом упражнении дана длина диагонали, т. е. AC = 2 см, вычислим сторону AB.
Имеем: AC² = AB² + BC² = 2AB (потому что AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> АВ = √2
Как вычислить диагональ прямоугольника
Прямоугольник — выпуклый четырёхугольник с четырьмя прямыми углами, параллелограмм с двумя равными диагоналями.
Свойства диагоналей прямоугольника
Диагонали прямоугольника обладают несколькими важными свойствами, которые полезны при решении задач, связанных с прямоугольниками и их диагоналями.
- Длина диагонали прямоугольника является гипотенузой прямоугольного треугольника, поэтому она равна квадратному корню из суммы квадратов двух сторон.
- Диагональ делит прямоугольник на два прямоугольных треугольника равной площади. Итак, диагональ прямоугольника является осью симметрии прямоугольника.
- Две диагонали прямоугольника равны и пересекаются в середине каждой линии, образуя 4 равнобедренных треугольника.
Формула расчета диагонали прямоугольника
Из приведенных выше свойств диагонали прямоугольника мы можем использовать теорему Пифагора для вычисления длины диагонали прямоугольника.
Предположим, у вас есть прямоугольник ABCD длиной a и шириной b, диагональ AC которого показана ниже.
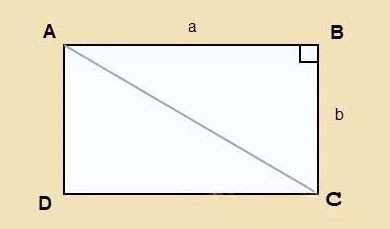
Применим теорему Пифагора к прямоугольному треугольнику ABC:
⇒ ⇒
Следовательно, диагональ прямоугольника длиной a и шириной b равна:
Итак, длина диагонали прямоугольника равна квадратному корню из суммы квадратов двух сторон (длины и ширины) прямоугольника.
Таким образом, мы можем вычислить диагональ квадрата или прямоугольника, просто применив теорему Пифагора.
Пример вычисления диагонали прямоугольника
Вычислите длину диагонали прямоугольника, длина которого 10 дм, а ширина 5 дм.
Решение:
Пусть длина диагонали прямоугольника равна a (a > 0, dm)
Применяя теорему Пифагора, длина диагонали прямоугольника равна:
а2 = 102 + 52 = 125
=> а = 5√5 дм
Пример, доказывающий, что четырехугольник является прямоугольником.
Свойства и формулу вычисления диагонали прямоугольника можно применить для решения некоторых задач, доказывающих, что четырехугольник является прямоугольником.
Дан четырехугольник ABCD, у которого две диагонали перпендикулярны друг другу. Пусть E, F, G, H — середины сторон AB, BC, CD, AD соответственно. Какую форму имеет четырехугольник EFGH? Почему?
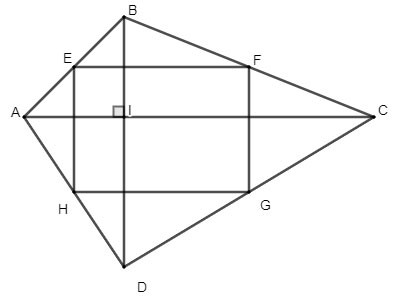
Решение:
Поскольку E — середина AB, H — середина AD.
=> EH — медиана треугольника ABD.
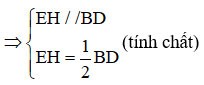 (1)
(1)
Поскольку F — середина BC, G — середина CD.
=> FG — медиана треугольника BCD
 (2)
(2)
Из (1) и (2) =>
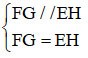
Рассмотрим четырехугольник EFGH.
ФГ // ЭХ
ФГ = ЭГ
=> EFGH — параллелограмм (опознавательный знак)
С другой стороны:
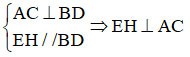
Также есть:
E — середина AB, F — середина BC.
=> EF — медиана треугольника ABC
=> ЭФ // АС
Но ЭН ⊥ АС => ЭН ⊥ EF
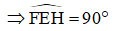
Параллелограмм EFGH имеет прямой угол
=> EFGH — прямоугольник



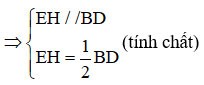 (1)
(1) (2)
(2)