В статье ниже Quantrimang.com подробно познакомит и поделится с читателями некоторыми материалами, связанными с темой формул для расчета объема конуса, боковой площади и полной площади конуса. Пожалуйста, ознакомьтесь с ним.
Оглавление
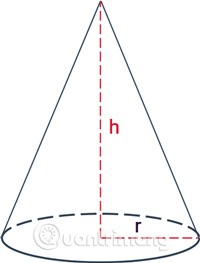
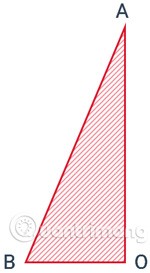
Пирамида образуется путем вращения прямоугольного треугольника вокруг своей оси (прямоугольной стороны) на один оборот.
Вычислите площадь конуса.
Площадь конуса часто называют двумя терминами: окружающая и полная.
- Боковая площадь конуса включает в себя только площадь поверхности, окружающей конус, но не площадь основания.
- Общая площадь вычисляется как величина всего пространства, занимаемого фигурой, включая боковую площадь и площадь круглого основания.
Конкретно следующим образом:
Если взять прямоугольный треугольник ABO в точке O, то вращение вокруг фиксированной прямой стороны OA даст конус.
- Ребро OB закругляется, образуя основание конуса, представляющее собой окружность с центром O.
- Ребро AB заметает окружающую поверхность конуса, каждое его положение называется образующей, например, AB является образующей.
- A — вершина, а AO — высота конуса.
|
 |
|
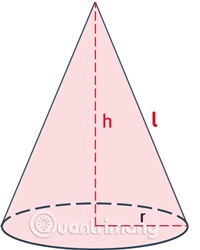
Формула для расчета боковой площади: равна половине произведения длины окружности основания на длину образующей.
 |
Применительно к конкретному примеру выше:
Там:
- Периметр — это площадь вокруг конуса.
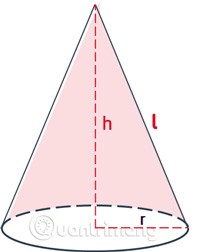
r— радиус основания конуса.l— длина образующей линии конуса.
|
Формула для расчета общей площади: равна боковой площади плюс площадь основания.
Рассчитайте объем конуса.
Объем конуса — это объем пространства, занимаемого конусом.
Формула для расчета объема конуса: равна 1/3 площади основания, умноженной на высоту.
Там:
Vобъем конуса.r— радиус основания конуса.hвысота — расстояние между вершиной и основанием конуса.
Определить генератор, высоту и радиус основания.
Высота — это расстояние от центра основания до вершины пирамиды.
Образующая — это расстояние от любой точки окружности основания до вершины пирамиды.
Поскольку конус образуется при повороте прямоугольного треугольника вокруг оси одной из его прямоугольных сторон один раз, высоту и радиус основания можно рассматривать как две прямоугольные стороны треугольника, а образующей — гипотенузу.
Следовательно, зная высоту и радиус основания, мы можем вычислить образующую линию по формуле:
Зная высоту и образующую, рассчитаем радиус основания по формуле:
Выше приведены формулы для расчета боковой площади, полной площади и объема конуса. Спасибо, что прочитали статью.