Давайте узнаем формулу для расчета боковой площади, полной площади и высоты цилиндра, чтобы применять ее в учебе и повседневной жизни.
Оглавление
Как рассчитать площадь цилиндра
Площадь цилиндра включает в себя боковую площадь и полную площадь.
Вы можете ввести высоту и радиус цилиндра в таблицу ниже, чтобы узнать боковую площадь и общую площадь цилиндра.
Формула для расчета площади боковой поверхности цилиндра
Боковая площадь цилиндра включает в себя только площадь окружающей цилиндр поверхности, не включая площадь двух оснований.
Формула для расчета площади боковой поверхности цилиндра — это длина окружности основания, умноженная на высоту.
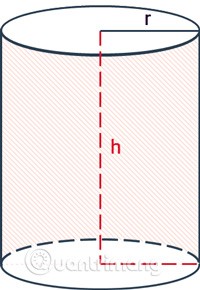 |
Там:
- Окружение — это прилегающая территория.
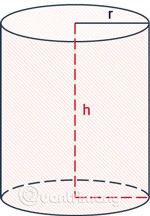
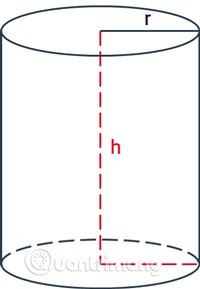
rрадиус цилиндра.h— высота, расстояние между двумя основаниями цилиндра.
|
Пример: 1
Круглый цилиндр имеет радиус основания r = 5 см, высоту h = 7 см. Рассчитайте площадь боковой поверхности вертикального цилиндра.
Решение: Площадь поверхности кругового цилиндра: Sxq = 2.π.rh = 2π.5.7 = 70π = 219,8 (см2).
Пример: 2
Дан квадрат ABCD со стороной 2a. Пусть O и O' — середины сторон AB и CD соответственно. При вращении этого квадрата вокруг оси OO' мы получаем вращающийся цилиндр. Рассчитайте площадь поверхности вращающегося цилиндра.
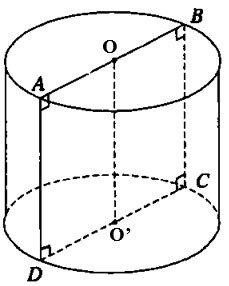
Решение:
Радиус окружности основания равен r= CD= a
Высота цилиндра h= OO'= AD=2a
Таким образом, боковая площадь цилиндра равна Sxq = 2πrh = 2π.a.2a =4a2π.
Формула для расчета полной площади цилиндра
Общая площадь рассчитывается как величина всего пространства, занимаемого фигурой, включая боковую площадь и площадь двух круговых оснований.
Формула для расчета полной площади цилиндра — это площадь боковой поверхности плюс площадь двух оснований.
Пример 1 : Рассчитайте общую площадь цилиндра с основанием 3 и высотой 5.
Решение:
Общая площадь равна Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Рассчитайте высоту цилиндра.
Высота цилиндра — это расстояние между двумя основаниями цилиндра.
Рассчитайте высоту цилиндра, зная его полную площадь и радиус основания.
Например: Дан цилиндр с радиусом основания R = 8 см и общей площадью 564π см2. Рассчитайте высоту цилиндра.
Приз:
У нас есть
Рассчитайте высоту цилиндра, зная площадь боковой поверхности.
=>
Формула для расчета радиуса основания цилиндра
1. Формула для вычисления длины окружности; площадь круга
Окружность имеет длину окружности C=2πr
=>
Круг с основанием имеет площадь S=πr2
=>
Например. Рассчитайте радиус основания цилиндра в следующих случаях:
а. Длина окружности основания равна 6π.
б. Площадь основания равна 25π.
Решение:
а. Радиус окружности основания равен
б. Радиус окружности основания равен
2. Основание — окружность, вписанная в многоугольник.
- Вписанный в любой треугольник: S - площадь треугольника, p - полупериметр.
- Вписанный в равносторонний треугольник: сторона
- Вписанный квадрат:
Пример 1 . Дан цилиндр, вписанный в куб с ребром а. Рассчитайте радиус этого цилиндра.
Радиус цилиндра равен:
Пример 2 . Дана правильная призма ABC.A'B'C' с объемом, описанным вокруг цилиндра. Рассчитайте радиус этого цилиндра.
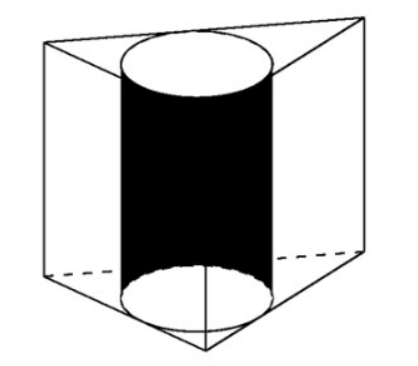
Объем призмы равен
Основание правильной призмы — равносторонний треугольник, поэтому => сторона
Следовательно, радиус основания цилиндра равен:
3. Основанием является окружность, описанная вокруг многоугольника.
Вписанный в любой треугольник:
Там:
- a, b, c — длины трех сторон треугольника.
- p — полупериметр треугольника:
Окружность прямоугольного треугольника: гипотенуза
Периферия равностороннего треугольника: сторона
Окружность квадрата: сторона
Например:
Вычислите радиус основания цилиндра, описанного около правильной пирамиды S.ABC, в следующих случаях:
а. ABC — прямоугольный треугольник с точкой A, где AB = a и AC = a√3.
б. ABC имеет AB= 5; АС= 7; БК=8
Приз:
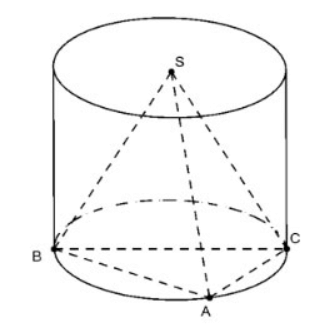
а. Гипотенуза
Так как ABC — прямой угол при A, радиус R=0,5.BC=a
б. Полупериметр треугольника ABC равен
Что такое круговой цилиндр?
Круговой цилиндр — это цилиндр с двумя равными круглыми основаниями, параллельными друг другу.
Цилиндры довольно часто используются в геометрических задачах от простых до сложных, в которых формула для вычисления площади и объема цилиндров часто используется по-разному. Если вы уже знаете, как вычислить площадь и длину окружности круга, вы легко выведете формулы для вычисления объема, боковой площади и полной площади цилиндра.
Формула для расчета площади поперечного сечения цилиндра
Разрежьте цилиндр плоскостью (P), проходящей через ось
- Полученное поперечное сечение представляет собой прямоугольник.
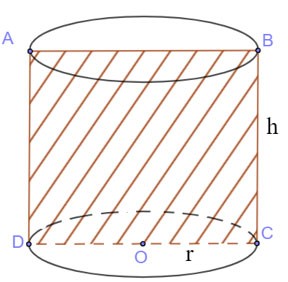 |
Площадь поперечного сечения:
SABCD = BC.CD = 2r.h
|
Разрежьте цилиндр плоскостью (P), параллельной оси и находящейся на расстоянии x от нее.
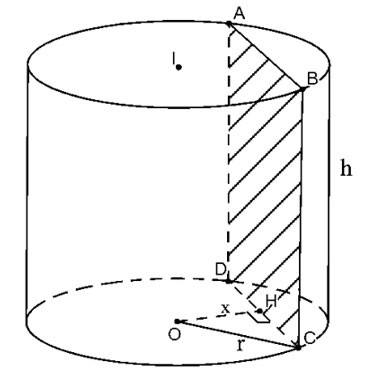 |
Полученное поперечное сечение представляет собой прямоугольник ABCD, как показано выше.
Пусть H будет серединой CD, тогда OH ⊥ CD=>
Следовательно, площадь поперечного сечения
|
Разрез цилиндра плоскостью (P), не перпендикулярной оси, но пересекающей все образующие цилиндра.
 |
Образованное поперечное сечение представляет собой окружность с центром O' и радиусом O'A'=r.
Площадь поперечного сечения: S= πr2
|
Разрез цилиндра плоскостью (Р), не перпендикулярной оси, а пересекающей все образующие цилиндра.
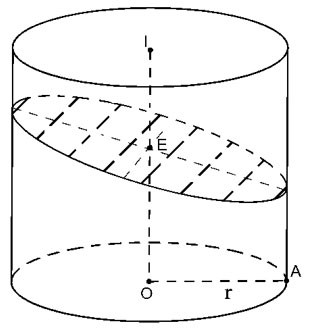 |
Полученное поперечное сечение представляет собой эллипс (E) с малой осью 2r => a=r.
Большая ось равна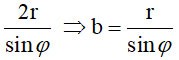
где 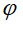 - угол между осью OI и (P) - угол между осью OI и (P)
Следовательно, площадь S= π. аб=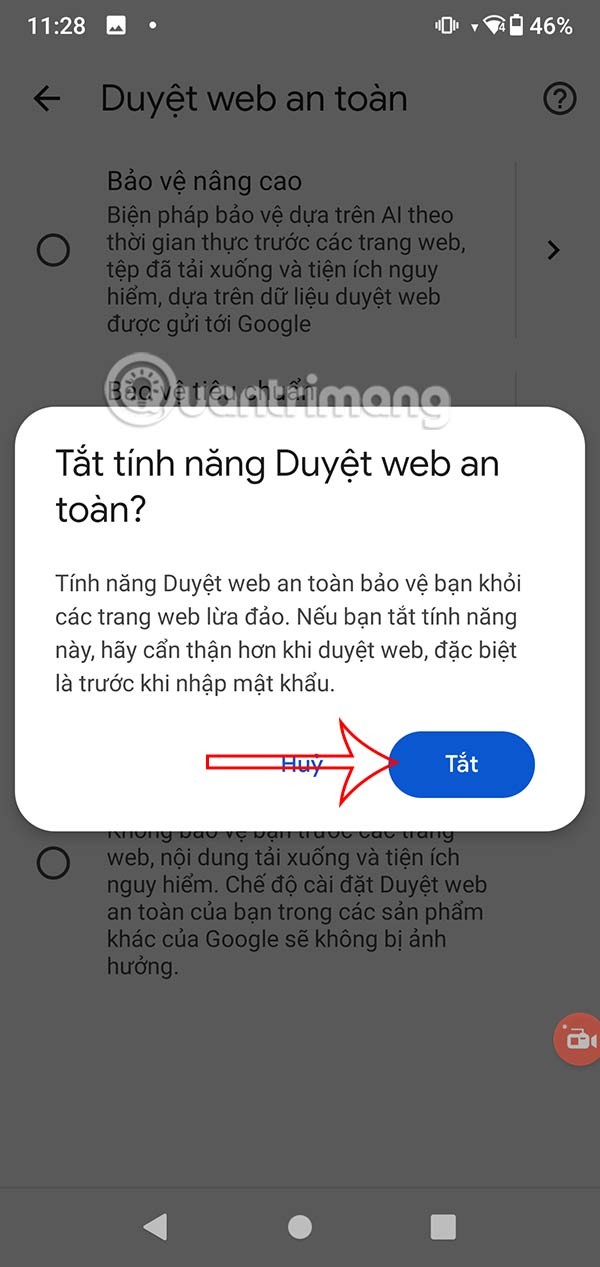
|
Пример расчета площади цилиндра
Урок 1 :
Боковая поверхность цилиндра имеет окружность основания 13 см и высоту 3 см.
Приз:
Имеем: длина окружности C = 2R.π = 13см, h = 3см.
Таким образом, площадь боковой поверхности цилиндра равна:
Sxq = 2πr.h = Ch = 13,3 = 39 (см²)
Урок 2 : Дан цилиндр с радиусом основания 6 см, а высота от основания до вершины цилиндра составляет 8 см. Какова площадь боковой поверхности и полная площадь цилиндра?
Премия
Согласно формуле имеем полукруг основания r = 6 см и высоту цилиндра h = 8 см. Таким образом, у нас есть формула для расчета боковой площади цилиндра и полной площади цилиндра следующим образом:
Площадь поверхности цилиндра = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 см²
Общая площадь цилиндра = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 см²
Урок 3 : Радиус основания цилиндра равен 7 см, а площадь боковой поверхности равна 352 см2.
Тогда высота цилиндра равна:
(А) 3,2 см; (Б) 4,6 см; (С) 1,8 см
(Д) 2,1 см; (E) Другой результат
Пожалуйста, выберите правильный результат.
Решение: У нас есть
Итак, ответ E правильный.
Урок 4 : Высота цилиндра равна радиусу окружности основания. Боковая площадь цилиндра составляет 314 см2. Рассчитайте радиус окружности основания и объем цилиндра (результат округлите до двух знаков после запятой).
Приз:
Боковая площадь цилиндра составляет 314 см2.
Имеем Sxq = 2.π.rh = 314
Где r = h
Итак, 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (см)
Объем цилиндра: V = π.r2.h = π.r3 ≈ 1109,65 (см³).
Надеюсь, статья выше помогла вам усвоить базовые и расширенные знания о цилиндрах, о том, как рассчитать общую площадь и боковую площадь цилиндра.









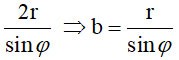
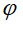 - угол между осью OI и (P)
- угол между осью OI и (P)